写在前面

很早就想写一篇博客记录调pid时的感受与所悟了，但是由于是静态博客，没法留下视频，所以一直认为没法形象的讲述调参过程，也一直盼望着能有什么虚拟调参软件练手。谁曾想一款陪伴了我11年的沙盒居然能给我这个契机。

为了照顾没有了解过minecraft的朋友或者说没有玩过valkyrien模组与computercraft的玩家，我先大致的描述一下为什么选用它们成为我的虚拟调参平台吧。mc是一款自由沙盒建造游戏，世界由方块和实体构成，方块允许着玩家自由改动，创造出丰富多彩的世界，实体一般是生物，受到重力以及浮力等物理影响。

这其实就是在说，原版mc中玩家可自由改动非实体世界的往往都是没有物理属性的，你甚至能见到一大片陆地浮在空中。而革命性模组valkyrien则赋予了方块物理属性，从此，玩家可以自由地与物理的世界交互了。至于computercraft模组，你可以理解为提供了集陀螺仪，加速度计等元件为一身的单片机，支持以lua为脚本的程序烧写，除此之外，它还能对所在物理结构进行力的模拟。

至此，我们可以实时获取物理结构的速度、姿态，也能对其施加力，一个闭环系统就有实现的可能了。

在此，我需要感谢up主发烧的烧的个人空间-发烧的烧个人主页-哔哩哔哩视频 (bilibili.com)对我提供的帮助，在我遇到困难时无私地帮我解惑，尽管我们并不认识。

准备工作

先给出几个模组地址

modrinth.com/mod/kotlin-for-forge

Valkyrien Skies - Minecraft Mod (modrinth.com)

CC: Tweaked - Minecraft Mod (modrinth.com)

CC: VS - Minecraft Mod (modrinth.com)

再介绍下valkyrien模组与computercraft的兼容附属模组CC:VS的几个API

以下都用”飞船”称呼物理结构

ship.getVelocity() 获取飞船在世界坐标系下x,y,z轴的速度

ship.getQuaternion()获取飞船姿态四元数

ship.getMass()获取飞船质量

ship.getMomentOfInertiaTensor()获取飞船惯性矩

ship.applyRotDependentTorque()给飞船一个局部坐标系下x,y,z轴的扭矩

ship.applyInvariantForce()给飞船施加一个世界坐标系下x,y,z轴的力

ship.applyRotDependentForce()给飞船施加一个局部坐标系下x,y,z轴的力

有了这些API，只要写好姿态解算与PID，就能实现飞控了

姿态解算

什么是四元数

高中时其实就学过二元数a+bi，可以在二维复平面上表示任意旋转

那么处于三维平面中，我们是否可以一个三元数a+bi+cj来表达任意旋转呢？

目前广泛的说法：三元数 - 维基百科，自由的百科全书 (wikipedia.org)

数学家哈密顿用了15年的时间都没找出正确的三元数形式，而是创造了四元数q=a+bi+cj+dk

使用球极投影的方式用四维空间中的旋转来表示三维中的旋转

四元数对向量的旋转作用

从四元数表示的旋转可以导出对应的旋转矩阵。给定一个单位四元数 q=w+xi+yj+zkq = w + xi + yj + zkq=w+xi+yj+zk，其对应的 3x3 旋转矩阵 R可以表示为：

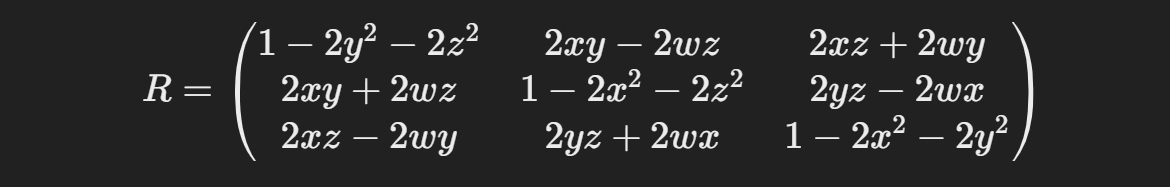
假设我们有一个向量 v，使用四元数旋转矩阵R可以得到旋转后的向量 v′

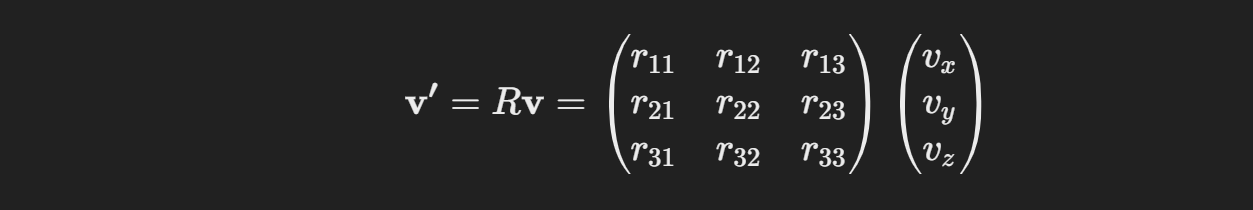
function RotateVectorByQuat(quat, v)
    local x = quat.x * 2
    local y = quat.y * 2
    local z = quat.z * 2
    local xx = quat.x * x
    local yy = quat.y * y
    local zz = quat.z * z
    local xy = quat.x * y
    local xz = quat.x * z
    local yz = quat.y * z
    local wx = quat.w * x
    local wy = quat.w * y
    local wz = quat.w * z
    local res = {}
    res.x = (1.0 - (yy + zz)) * v.x + (xy - wz) * v.y + (xz + wy) * v.z
    res.y = (xy + wz) * v.x + (1.0 - (xx + zz)) * v.y + (yz - wx) * v.z
    res.z = (xz - wy) * v.x + (yz + wx) * v.y + (1.0 - (xx + yy)) * v.z
    return res
end

四元数转欧拉角速度

四元数反映了在世界坐标系下姿态的一次旋转

先将x轴与z轴的单位向量以这次四元数进行旋转得XPoint与ZPoint

然后对上一次四元数的三个虚部取负数，即求共轭四元数，这表明了上一次四元数的逆旋转

再对XPoint与ZPoint进行这逆旋转即可得到两次旋转的差值，这个差值已经能反映姿态变化率了

我们将其转化为欧拉角

如图所示，请在脑海中相向它的转动与各个向量的分量所在

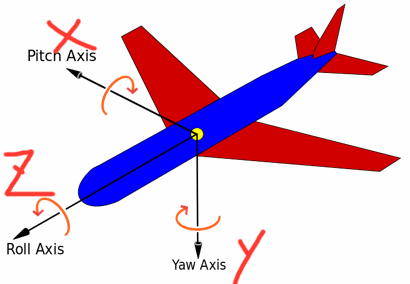
z向量是飞船头指向的轴，对它的y分量求反正弦函数可以算得俯仰角

x向量是分机翅膀所在的轴，同理我们也会通过它的y分量求滚转角

最后通过x向量的z分量与x分量的反正切求偏航角

local function getEularRate(q)
    local quat = q
    local omega = {}
    local pX = RotateVectorByQuat(quat, { x = 1, y = 0, z = 0 })
    local pY = RotateVectorByQuat(quat, { x = 0, y = 1, z = 0 })
    local pZ = RotateVectorByQuat(quat, { x = 0, y = 0, z = -1 })

    local XPoint = { x = pX.x, y = pX.y, z = pX.z }
    local ZPoint = { x = pZ.x, y = pZ.y, z = pZ.z }
    preQuat.x = -preQuat.x
    preQuat.y = -preQuat.y
    preQuat.z = -preQuat.z
    XPoint = RotateVectorByQuat(preQuat, XPoint)
    ZPoint = RotateVectorByQuat(preQuat, ZPoint)
    omega.pitch = math.deg(math.asin(ZPoint.y))
    omega.roll = math.deg(math.asin(XPoint.y))
    omega.yaw = math.deg(math.atan2(-XPoint.z, XPoint.x))
    preQuat = quat
    return {
        r = omega.roll,
        y = omega.yaw,
        p = omega.pitch
    }

PID算法

什么是PID算法

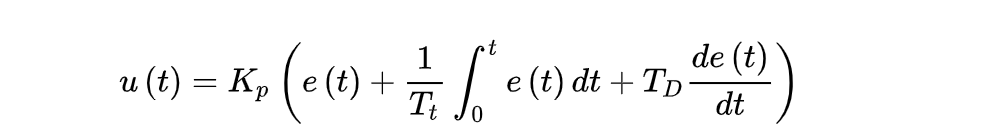
可以举例来解释：我想控制飞船在x轴的前进速度为50，我能给飞船一个x轴正方向上的力F，pid算法实现的就是根据实时速度的反馈来计算F应该的大小是多少，使得实时速度最后控制在50

假设一个采样周期是t

比例参数p

1	Fp = kp*Error

力大小与误差成正比，且当速度比目标小的时候力为正值，当当速度比目标大的时候力为负值，其中kp是比例系数。

比如说当前实际速度为30，**并且假设给多大的力增加多大的速度(线性的且比例为1)*，此时误差为20，经过一个t后实际速度为30+20kp。

假设kp为0.5，那么下次的速度就是40，然后就是45，永远趋近与50而到不了50，这便是kp太小而导致的失调

假设kp为1.5，那么下次速度就是60，然后就是45，永远会在50附近震荡而到不了50，这便是kp太大而导致的超调

假设kp为1，那么下次速度正好是50，但是由于一些原因，这往往并不能实现系统的精确控制，而且诸如位置环来说力的大小与位置改变的关系并不是线性的，我们在下一个参数中接着讲

微分参数d

系统会有一定延时，在现实生活中，一个大小的力并不是瞬时就给上的，就算不在现实，哪怕是在虚拟中，指令执行也有一定延迟。具体例子就是，采样周期稍微比理想时间长点或短点，本该就会导致实际值落在50.00001或49.99999，这样仍然会有误差，从而导致震荡。

况且kp的适当增大能提升系统的响应速度，有时候些许的震荡总比所谓刚刚好的值带来的稳态误差要好(第三个参数时会讲到)

所以既然在单kp的情况下震荡出现往往不可避免，那么我们就要那么就必须引出下一项参数

1	Fd = kd * dError/dt

即这个力与误差的变化速度有关。假设目标速度不变，实际速度变大时误差减小，即误差变化速度为负，那么力为负；反之当实际速度变小时误差也减小，那么力为正。也就是说Fd是阻碍误差减小的力，误差减小的越快阻尼就越大。

由于误差减小的力始终受到一个阻尼，所以飞船速度震荡幅度会快速缩小

kd的失调就是并没有明显的缓解kp的震荡

而kd的超调可能会导致对误差的变化率过于敏感，从而放大误差的快速变化（如噪声），导致高频震荡

找一个明显缓解kp的低频震荡而不会产生高频震荡的值就是合适的kd值

积分参数i

上面两个参数在理想情况下已经能使飞船速度控制在50了，

虽然游戏中没有空气阻力，但是不代表游戏里没有其他干扰力，如果我们把刚刚探讨的轴换成y轴，就会出现一个重力开始影响系统

是想一个情况，假设现在飞船达到上升速度50还需要一个系统给的力为10，而飞船受到的重力恰好为10，那么就有一个尴尬的情况诞生了，飞船y轴合力始终为0，所以速度也不变，系统始终拥有一个稳定的误差使其无法达到50速度。

这便是稳态误差情况，解决的办法就是积分值

1	Fi = ki * 积分号(Error)/dt

只要误差存在，就不断地对误差进行积分，并反应在调节力度上。

这样当稳态误差发生时，还有个不断增大的力可以消除它

只不过参数ki的引入会带来积分过饱和等问题，在一些不那么需要精确控制的场合用PD控制器即可

ki的失调无法消除稳态误差’

ki的超调则会同样会产生震荡

PID实现飞行器

实际游玩中飞船的姿态精确性并不需要那么高，3以下的偏差往往可以接收，除了y轴上的重力影响要用到积分I之外，使用PD控制器完全能胜任大部分需求（其实y轴影响也没那么大啦，除了飞船会及其微小的向下掉），下面给出一个基本的PID控制器的写法，其中max用于对系统进行限幅，防止输出过大值(不过游戏中实测没啥必要)

function PIDController(kp, ki, kd, setpoint, measurement, prev_error, integral,max)
    local error = setpoint - measurement

    local proportional = kp * error

    integral = integral + error
    local integral_term = ki * integral

    local derivative = kd * (error - prev_error)

    local output = proportional + integral_term + derivative

    if output > max then
        output = max
    elseif output < -max then
        output = -max
    end

    return output, error, integral
end

世界坐标系下的x,y,z轴速度闭环

很简单，不赘述了

function setShipWorldVelo(x,y,z)
    local v = ship.getVelocity()
    local M = ship.getMass()

    outputx, new_errorx, new_integralx = PIDController(kp, 0, kd, x, v.x, prev_errorx, integralx,max)
    outputy, new_errory, new_integraly = PIDController(kp, ki, kd, y, v.y, prev_errory, integraly,max)
    outputz, new_errorz, new_integralz = PIDController(kp, 0, kd, z, v.z, prev_errorz, integralz,max)

    prev_errorx = new_errorx
    integralx = new_integralx
    prev_errory = new_errory
    integraly = new_integraly
    prev_errorz = new_errorz
    integralz = new_integralz

    ship.applyInvariantForce(outputx*M,outputy*M,outputz*M)
end

局部坐标系下的x,y,z轴速度闭环

通过

function RotateVectorByConjugateQuat(q, v)

  local conj = { w = q.w, x = -q.x, y = -q.y, z = -q.z }

  return RotateVectorByQuat(conj, v)

end

得到局部坐标系速度，这样才可以和applyRotDependentForce做闭环

function setShipRotVelo(x,y,z)
    local q = ship.getQuaternion()
    local v = ship.getVelocity()
    v = RotateVectorByConjugateQuat(q,v)
    local M = ship.getMass()

    outputx, new_errorx, new_integralx = PIDController(kp, ki, kd, x, v.x, prev_errorx, integralx,max)
    outputy, new_errory, new_integraly = PIDController(kp, ki, kd, y, v.y, prev_errory, integraly,max)
    outputz, new_errorz, new_integralz = PIDController(kp, ki, kd, z, v.z, prev_errorz, integralz,max)

    prev_errorx = new_errorx
    integralx = new_integralx
    prev_errory = new_errory
    integraly = new_integraly
    prev_errorz = new_errorz
    integralz = new_integralz

    ship.applyRotDependentForce(outputx*M,outputy*M,outputz*M)
end

局部坐标系的x,y,z轴角速度闭环

姿态解算上面说过了，拿到角速度自然就能做闭环了

function setShipOmega(r,p,y)
    local q = ship.getQuaternion()
    local eulerAngles = getEularRate(q)
    local I = ship.getMomentOfInertiaTensor()[1][1]

    outputr, new_errorr, new_integralr = PIDController(kp2, 0, kd2,r, eulerAngles.r, prev_errorr, integralr,max2)
    outputp, new_errorp, new_integralp = PIDController(kp2, 0, kd2,p, eulerAngles.p, prev_errorp, integralp,max2)
    outputa, new_errora, new_integrala = PIDController(kp2, 0, kd2,y, eulerAngles.y, prev_errora, integrala,max2)

    prev_errorr = new_errorr
    integralr = new_integralr
    prev_errorp = new_errorp
    integralp = new_integralp
    prev_errora = new_errora
    integrala = new_integrala

    ship.applyRotDependentTorque(outputp*I,outputa*I,outputr*I)
end

形状与质量适配

这部分内容已经出现在上面的代码中，现在详细解释下：

F = Ma

其实与其把速度环系统的输出看成力，不如看成加速度，这样只要在输出乘上API拿取的飞船质量M即可适应任何质量的飞船

τ=I α , 这个公式指扭矩(可以看成专门对旋转的一个作用)的大小等于惯性矩的大小乘上加速度

这下可能有人要释怀的笑了：因为旋转与质量无关，这个公式又几乎与上面的牛顿第二定律相似

飞船形状影响着惯性矩，惯性矩又反映了旋转的难易程度，我们完全可以把角速度环的输出看成加速度，这样在输出时乘上API拿到的惯性矩，此时即可适应任何形状的飞船

后记

可以尝试的后序过程：结合之前写的Boids算法在mc中实现蜂群无人机，想想就很酷

文章写的很累，可能会有些小漏洞，遇到奇怪的地方请见谅

链接推荐：

控制器模组：Create: Tweaked Controllers - Minecraft Mod (modrinth.com)
CC模组文档：CC: Tweaked
我的代码仓库地址：varkyrien_cc_ship

TangSong404's Blog

PID飞控，但是Minecraft