我的学习项目例程与数据集将持续分享至ML_study_repo仓库中

线性回归

概率密度函数推导

$目标值与误差的关系是特征向量$

$误差独立同分布，其概率服从标准正态分布均值为且方差为$
$由标准正态分布公式$
$得到$
$由、得在给定与时目标值的条件概率服从方差为且均值为的正态分布$

最大似然值推导（最小二乘法）

$想象一下，你有一套模型参数，你想知道在这些参数下，观测到数据点有多么可能。$
$为此，你需要计算每个数据样本在模型中的可能性并综合，来衡量这些参数是否适合所有数据点。$
$由于独立性的假设，这些概率可以通过相乘来组合，乘积被叫做联合概率$
$而此时有关的函数被叫做似然函数，用来衡量某个参数的拟合程度$
$通过求似然函数的极值，便能找到最优参数$
$由上，似然函数理解为特定下所有概率的乘积$

$对似然函数取对数，化乘法运算为加法运算$

$对后半段部分进行矩阵化方便计算$
$得到$
$求偏导$

$令求最大似然值点$
$得$

梯度下降法

$最大似然函数的直接求解涉及到求的逆矩阵，具有的时间复杂度$
$其中是特征数，计算成本高，甚至无解，所以需要梯度下降法求解。$
$推导出的似然值核心项为$
$为了消除样本数量的影响，梯度下降的目标函数还要求个平均：$
$梯度下降法的最终目的也就是对这个目标函数求得一个近似最优值：$
$对求偏导得到：$
$化简得到：$
$这就是趋向于新的最优点的梯度，给梯度乘上一个学习率，所以新参数$
$这是批量梯度下降的公式，迭代速度往往非常慢，于是有了随机梯度下降$
$但是随机梯度下降并不一定每次都沿着收敛的方向，所以就有了小批量梯度下降法：$

$上面公式中的就是一次迭代的样本数，也就是我们常说的$

模型评估方法

$线性回归模型的评估用到的是统计学中的决定系数，其值由回归平方和与总平方和之商得到$
$总平方和：，即实际值与平均值差的平方和$
$回归平方和：，即预测值与平均值差的平方和$
$残差平方和：，即预测值与实际值差的平方和$
$最后决定系数有两种表示方式$

$或$
$还有其他的标准$
$均方误差：$
$均方根误差：$
$平均绝对误差$
$如果的值是，意味着平均而言，每个预测值与实际值的偏差约为个目标变量单位$
$与单位相同，对异常值的敏感性更高，更容易被离群点影响，比直观$

非线性回归

$非线性回归与线性回归的主要区别在于，非线性回归中与遵循某种非线性函数形式。$
$即公式不再是：$

$而是类如以下的：$

$其中的往往都是不同的参数向量，它们的维度与的维度相当$

标准化

$为什么要在数据预处理时标准化：$
$如果直接用原始指标值进行分析，就会突出数值较高的指标，削弱数值水平低指标的作用；$
$标准化处理后，各指标值处于同一数量级别，便于分析。$
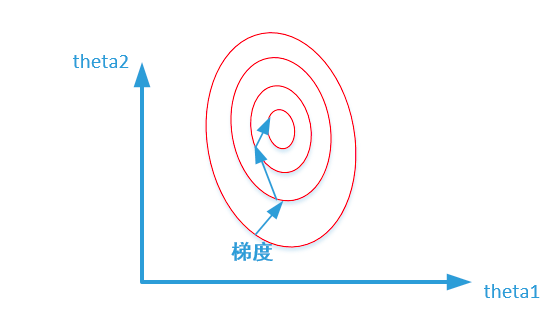
$梯度下降法时，标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度$
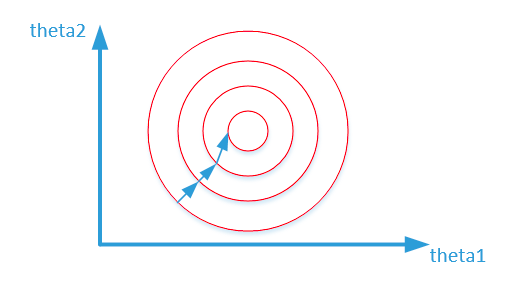
$如下图所示，正圆下降速度显然更快。$
$标准化的方法：原始数据减均值之后，再除以标准差。将数据变换为均值为，标准差为的分布$
$公式：，其中求标准差：$

正则化

$为什么要在目标函数中使用正则化先来说说过拟合：$
$过拟合原因：数据噪声太大；特征太多；模型太复杂$
$过拟合的解决办法：清洗数据减少模型参数降低模型复杂度正则化减少参数的大小。$
$如何做到正则化：$
$正则化，即回归，公式$
$正则化，即岭回归，公式$
$其实正则项本质是个惩罚因子，将参数绝对值和或平方和掺到代价函数中，可以有效抑制过大的参数$
$两种正则化的区别：$
$对绝对值大的权重予以重惩，当权重绝对值趋近于时基本不惩罚。$
$即越大的数，其平方越大，越小的数，比如小于的数，其平方反而越小；$
$正则化对所有权重予以同样惩罚，较小的权重在被惩罚后就会变$
$模型训练好后，这些权值等于的特征可以省去，从而达到模型稀疏化的效果。$
$原因按求导直观来看：$
$求的梯度为，它的减小速率随着自身减小而不断减小，所以永远趋近于零而不会到达零；$
$而的梯度则为，可以理解为减小速率始终是个常数，最终会减到$
$更适合防止过拟合，使网络更倾向于使用所有输入特征，而不是严重依赖输入特征中某些小部分特征$
$则更适合特征选择，即稀疏化操作$

逻辑回归

逻辑回归概率密度函数推导

$对于经典二分类问题，目标值只有与，而回归本身的预测结果并非是两个值$
$所以我们可以把预测结果映射到这个区间内，成为一个置信度，或者说概率；$
$如推断出图片中的动物是猫的置信度为，也就是说图中动物有成概率是猫，就可以认为归到了猫类。$
$把预测的结果映射到内可以通过函数$
$令，在给定与时的概率密度函数就是$

$同样举个例子，可以认为是把分到猫类的概率，类别为猫类；$
$那么类别就是狗类，就是分到狗类的概率$

最大似然与梯度下降

$同线性回归最大似然值如何推导那般，我们可以得到$

$取对数得到：$
$以上就是最大似然值，我们要求它的最大值；先求个平均再取反方便梯度下降$
$得到代价函数：$
$进行梯度下降，求偏导：$

$所以新参数$

多分类逻辑回归sigmoid

$当如上方使用函数进行所谓的多分类逻辑回归，不过是进行多次二分类逻辑回归$
$举个例子，要将桌面上一堆不同的小球分为红黄蓝三类$
$应当先进行一次红色，非红色的双分类逻辑回归，计算出是红色类别的概率$
$然后再针对蓝色，黄色都进行一次$
$得到诸如的结果，这表示着小球是红色的$
$假如数据样本为，总共有类别，我们想要的结果应该是，所以参数应该是$
$上面这个例子说明了多分类逻辑回归时矩阵大小一般的设定$
$其评估系数一般为在测试集上准确率，其损失一般使用交叉熵见下方详述$

信息熵与交叉熵

$对于一个长度为的二进制编码，其所能表达的可能事件数量为。$
$信息论的创始人香农很早就想到了这点，他将二进制编码的长度称为信息量。$
$一般来说，明确有种可能的事件所需要的信息量为。$
$为了便于理解，我们在均匀分布的假设下延申，对于某个事件发生的概率，可以对应的可能事件数量为$
$。$
$再说回信息量公式，则可以推出单个事件的信息量为$
$而对于整个系统，需要计算每个事件发生的概率乘以其信息量，即。$
$在一组可能事件中，每个事件发生的概率分布所包含的信息量，称之为信息熵，这就是大名鼎鼎的香农公式：$

$再说到交叉熵，它常用于衡量两个概率分布之间的距离。$
$它反映了用一个预测分布来或近似另一个真实分布时的代价。$

$交叉熵表示用预测分布编码真实分布的平均编码长度。其值越小，说明拟合越好。$
$如果，即预测分布完美等于真实分布，交叉熵等于的熵$
$如果偏离交叉熵会大于真实分布的熵，增加的部分称为相对熵（散度）$
$在上方二分类代价函数其实已经使用到了这一点：$

多分类逻辑回归softmax

$公式本质上是求该类别值在所有类别上的占比，如$
$由于值本身可能差异可能并不大，导致占比区分不明确，所以我们需要尽可能放大这一差异$
$于是乎公式就变成了这样：$
$其代价函数同样使用交叉熵函数是类别数量$
$同样地求偏导梯度下降计算新参数，得到$

$很显然与的梯度下降是一致的，区别仅在于激活函数的不同$

两种激活函数的比较

特性	Sigmoid	Softmax
适用场景	多标签分类，一个数据可以分到多类	单标签分类，一个数据只能分到一类
类别独立性	每个类别概率独立预测，互不影响	类别间有概率竞争关系，概率总和为 1
输出范围	每个类别的概率在 [0, 1]	概率分布，总和为 1
典型任务	图像多标签分类，文本情感分析	图像单标签分类（如手写数字分类）

TangSong404's Blog

机器学习数学理论(i)——简单的回归问题