机器学习数学理论(ii)——聚类与决策树

我的学习项目例程与数据集将持续分享至ML_study_repo仓库中

聚类算法

KMeans聚类

介绍

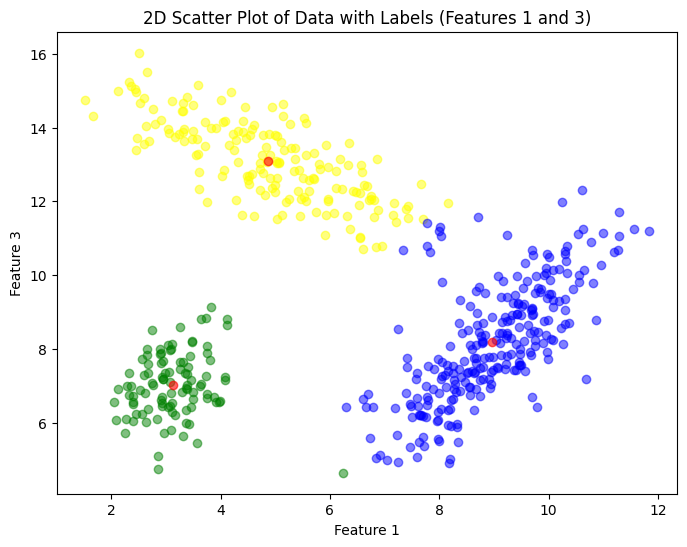
所谓聚类就是在没有标签的情况下分类，KMeans可以算作一种最简单的聚类算法

然而由于其初始质心的随机性**(见工作流程)**，有时得到的可能是局部最优解，且相同数据每次训练的结果都可能不一样,存在着一定局限性

工作流程

1. 首先需要确定最后簇的个数N，即最终要分为几类
2. 随机抽取数据中的N个点，作为初始的簇质心
3. 针对其它的每个样本点，分别找到离它们最近**(最近可以用多种方式来衡量，如余弦最近或者欧式距离)**的簇质心，将它们划分到该簇中
4. 根据每个簇内所有的数据，计算出新的簇质心
5. 重复3、4步骤直到质心的变化小于一定值完成聚类

评估方法

使用KMeans算法时，在没有标签的情况下对训练结果进行评估，我们可以使用以下两种方法：

• Inertia(簇内平方和)

Inertia越小，代表着簇内样本越相似，聚类的效果就越好

其实这个公式很类似于SSE(残差平方和)，只不过将当前数据与质心之差看作了真实值与预测值之差

将每个簇的Inertia相加就得到了整体平方和，这可以用作对模型整体水平的一个衡量

• 轮廓系数

若S(i)接近1，说明b(i)远大于a(i)，证明了样本i聚类合理

若S(i)接近0，说明b(i)与a(i)值差不多，证明了样本i在边界点

若S(i)接近-1，说明a(i)远大于b(i)，证明了样本i更应该分到别的簇

针对所有样本的轮廓系数求平均就能得到模型整体水平的一个衡量

DBSCAN聚类

介绍

DBSCAN是另一种常见的聚类方法（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）

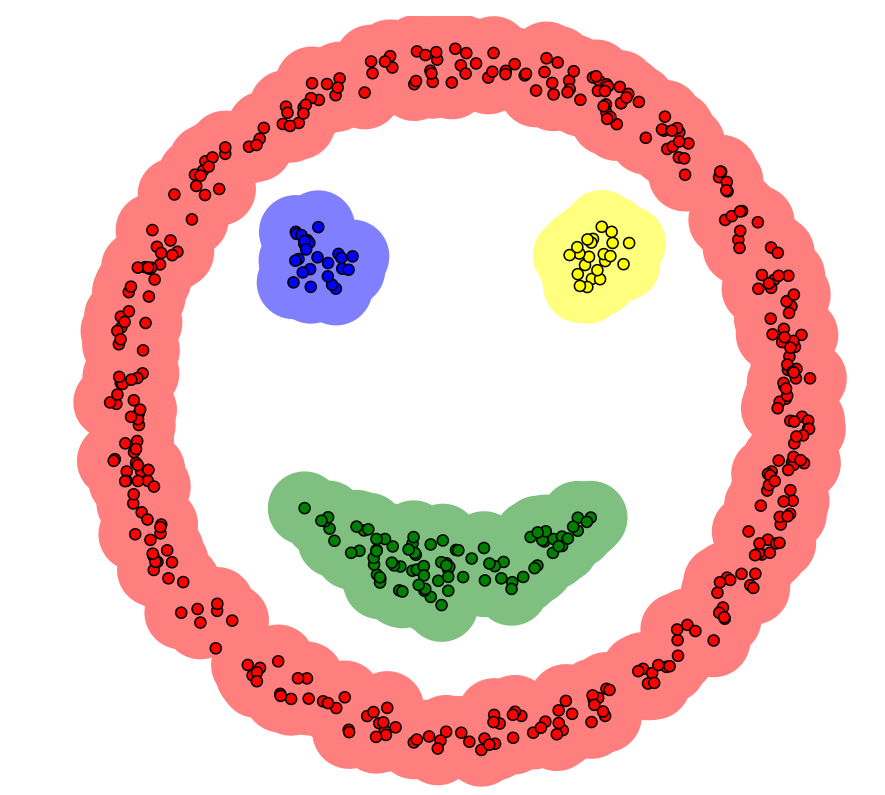
该算法将具有足够密度的区域划分为簇，所以它支持发现任意形状的簇，并且不需要像KMeans一样预设定簇的个数

工作流程

先说一个概念，对于一个数据点，以其为圆心，半径为radius的范围内，如果点数超过density，则说明它是一个核心点，否则就是一个离群点

其中radius，density就是DBSCAN算法的参数

1.首先在样本中随机找到一个核心点，作为一个簇C的第一个点

2.对这个核心点范围r内的所有点进行是否为核心点的判断，如果是就放入簇C中

3.对簇C中的所有点都执行第2步操作，直到不是核心点或者该点已经存在于C中（其实就是一个生长的操作，在密度小的地方会断掉）

4.此时簇C已经完成聚类，对剩下的样本重新开始第1步以开始新的簇聚类，以此类推，直到只剩下离群点和已经聚类的点

决策树算法

和上方聚类算法做个分割防止误解，决策树属于监督学习，所以是有标签的

先从分类决策树讲起方便理解

原理

想象一下，我们平时是怎么对一些事物分类的。

以猫狗虎三种动物为例，如何区分它们：

1.根据科来判断，猫科是猫、虎，犬科是狗

2.猫、虎根据体型判断，大的是虎，小的是猫

决策树的预测正是如此，通过不同特征一步步切分数据集将某一个样本最终确定在一个类别上的。

如下图例子所示，4个样本根据2个特征最后被分到了A,B二类

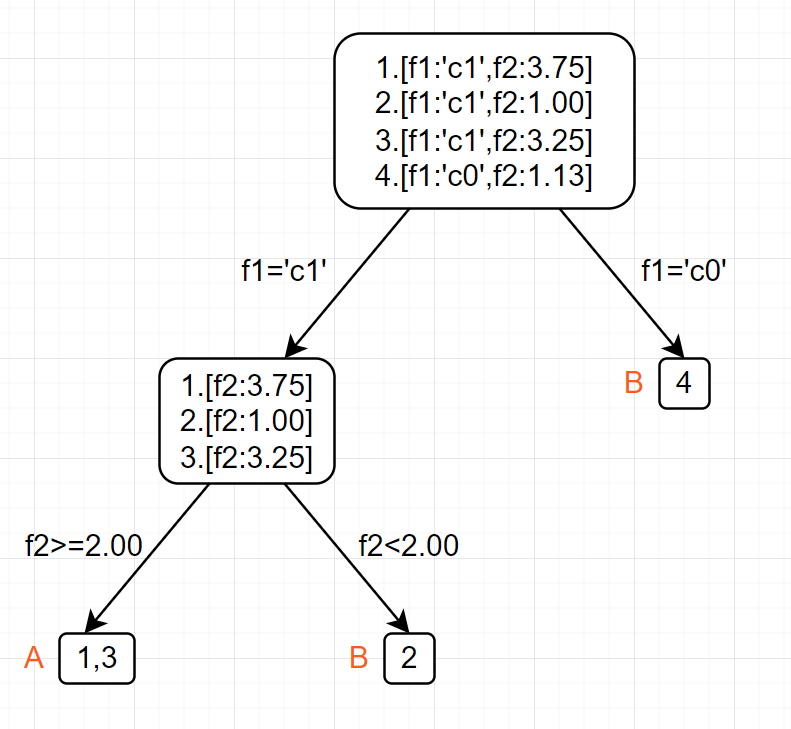
这个树是如何生长出来的呢？继续向下看

训练过程

根据原理中的例图可以发现，决策树每次进行分支都是根据特征进行的，所以特征的选取及其分割依据就非常重要

看完下面的笔记你就知道了决策树是如何自己按序选择特征及其分割依据的

特征选取的顺序

决策树是贪婪算法，它在每一步选择局部最优的特征进行分裂。一旦一个特征被用于分裂，它就不会在后续节点中再次被考虑。因此，早期选择的特征对树的结构影响更大，它们决定了后续特征的选择空间。

同上方一样的4个样本，如果我们采用现在这样先f2后f1的区分顺序，就会产生下图的树形结构

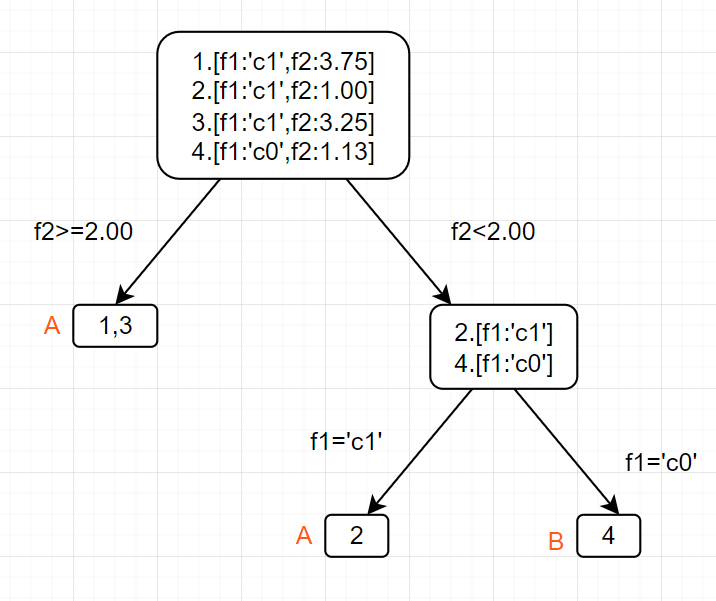
显然f2有某种重要性，先使用它分类时可以更早的把更多数据划到正确的类别（1，3两个数据直接划到A类）

这种重要性我们可以用一个叫做信息增益的概念衡量

信息增益

信息增益 = 这次分割前的熵 - 分割后的熵

此处的熵为所在数据集内标签所含有的熵，如标签为[A,A,A,A,B,B]，其熵就是这个数组的香农熵

先来算一下原始数据的熵。

看一下第一次分类后的熵

• 采用f1在前的顺序
  
  右侧节点只有一个B类所以熵为0

  再乘上两侧的样本数量占总数量比例
  

• 采用f2在前的顺序

左侧节点为一类熵为0

再乘上两侧的样本数量占总数量比例

两种顺序信息增益分别为f2在前时0.311，以及f1在前时0.1225

于是我们选择f2在前的顺序，因为其分类效果更好，通过它分类后两类数据的熵更小

连续特征分割

像f1这样的特征我们称为离散特征，对于它们的处理非常简单，根据其所有的情况进行分割即可

而f2这样的我们成为称为特征，我们需要找到一个数值点P来进行划分，<=P的分到一侧，>P的分到另一侧

找P的逻辑

先对该连续特征的所有值进行排序

取每两个点的中点作为所需要的P进行尝试，并最终找到分割后信息增益最大的作为真正的数值点

如[1.00,1.13,3.25,3.75]这样的特征值，一般会选择[1.065,2.19,3.5]作为所需要的P

最后计算出按照<=2.19以及>2.19进行分割时信息增益最大，所以选择其为f2的分类依据

（注：例图上的分割数值是我随便给的，所以和这里不一样）

指标历程与剪枝

指标

分割前后评估的指标有多种版本

ID3 (信息增益)

这就是我们上面使用的信息增益算法，但是它有个重大的问题：假设一个离散特征的可取值很多，比如说“用户ID”，这种算法会优先选择以该特征作为分割依据，出现大量分支，破坏树的结构。即使这不是一个有意义的特征。但毕竟这样分确实是熵最小的

C4.5 (信息增益率)

信息增益率(特征A) = 信息增益(特征A) / 分裂信息(特征A)

分裂信息(特征A) = 对于整个特征A来说，不同取值所带来的熵，如特征A值为[1,1,1,2,3,3]，其分裂信息就为[1,1,1,2,3,3]的熵

一个离散特征的可取值很多，导致其的分裂熵会很大，对指标起到了一个很好的惩罚作用

这能很好的解决信息增益的问题

CART (基尼系数)

基尼系数衡量的是数据集的纯度，基尼系数越小，数据集纯度越高。计算速度比信息增益率更快

基尼系数(D) = 1 - ∑[p(i)^2] ,p(i)是D中属于类别i的样本比例

剪枝

以下说到的泛化性能往往都是在测试集上评估的指标

预剪枝就是在构造决策树的过程中，先对每个结点在划分前进行估计，若果当前结点的划分不能带来决策树模型泛化性能的提升，则不对当前结点进行划分并且将当前结点标记为叶结点。

此外还可以通过以下方法预剪枝

• 限制树的深度: 设置树的最大深度，当树达到指定深度时停止生长。
• 限制叶子节点的最小样本数: 设置每个叶子节点必须包含的最小样本数。如果一个分裂导致某个叶子节点的样本数小于阈值，则停止分裂。这可以防止生成过于细粒度的规则，从而减少过拟合。
• 限制分裂的最小信息增益/基尼指数降低: 设置一个阈值，只有当分裂带来的信息增益或基尼指数降低大于阈值时才进行分裂。这可以避免对模型改进很小的分裂。

后剪枝就是先构造一颗完整的决策树，然后自底向上的对非叶结点进行考察，若将该结点对应的子树换为叶结点能够带来泛化性能的提升，则把该子树替换为叶结点。

回归决策树

我们刚刚一直说的都是用于分类的决策树

回归决策树其实也是与分类决策树一样的思路。它将特征空间划分为多个矩形区域，并在每个区域内用一个常数（叶节点的值）进行预测

它最大的特点就是“分段线性”

与此同时，它也无法对训练数据外的数据作很好的延申预测，只能很好地在已有的数据间插值。

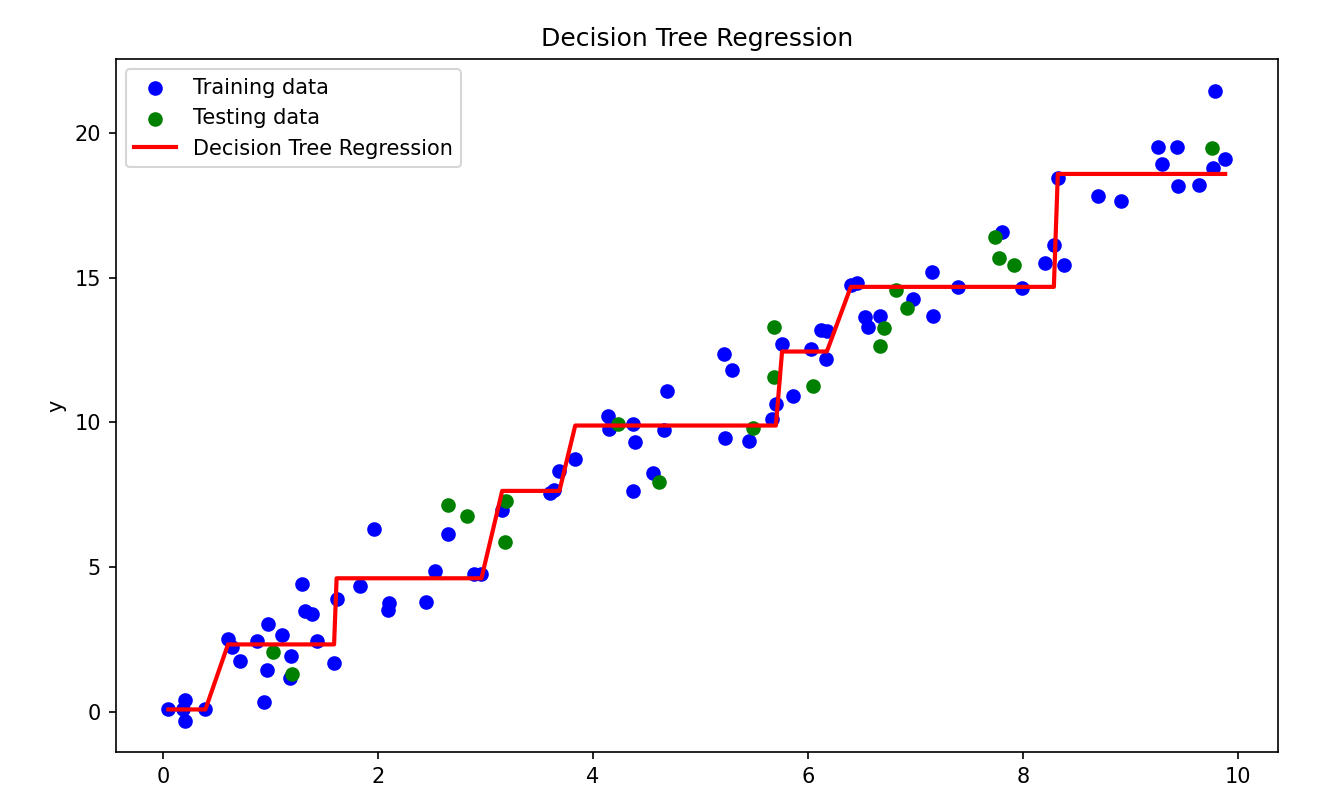
回归决策树的指标不再是上面说到过的指标了，而是回到了MSE

它同分类决策树一样找到效果最好的特征以及分割依据，在数据集切割到只剩一个样本或者没有特征可用的时候返回当前数据集标签的均值作为树最底端节点的值

因此回归树预测时的结果一定是树底端节点值中的一个，这映证了我们说的回归决策树无法对训练数据外的数据作很好的延申预测